Coding is only one part of programming. As my own approach to programming has matured, I have found myself thinking about a potential problem more before I dive in. Making time to imagine possible solutions before the actual coding begins can be instructive. But it’s also important to know when to start work. In this post, I consider what this thinking process looks like for me through imagining a maze or labyrinth-based game. I walk through the process of starting to make a game.

Inspiration

A few weeks ago, I was watching From Bedrooms to Billions on Netflix, a documentary about the birth of video game development and its transition from a craft to an industry.

12 minutes into the film, there’s mention of a basic but scary game called 3D Monster Maze, developed for the Spectrum ZX81, released by JK Greye Software in 1981.

Memories

I remember playing this game. It may be that I have only ever played an emulation rather than the original but it left its mark.

I inherited a Spectrum from my cousin as a hand-me-down many years after it came out, but I don’t remember playing much of anything on it much less 3D Monster Maze. By that time, my brothers and I were playing on our second-hand Master System and I was coding in QBasic on my first PC, a 386. But I remember the fear I felt when I played this game, whichever system it was on and dated as it was even at that time.

Screenshot from _3D Monster Maze_, believed to be fair use as part of a critique about the game.

You can actually play the game yourself by going to this Spectrum ZX81 emulator and typing LOAD "3DMONSTERMAZE". Edge magazine published, in April 2006, an article about the making of 3D Monster Maze, republished on the website Sockmonsters.

Starting to think

I am, for many reasons, curious about this simple but scary game. Specifically, I started to to think about the kind of approach one could take to writing a simple but decent maze-based game, like this one.

I’m sure others have tackled this before and in a much more elegant and interesting way than the one I’m about to outline here. But, as other bloggers and vloggers keep maintaining, coding is only part of the job of programming – a lot of it is about thinking and planning. With that in mind, how would I develop a similarly simple but interesting maze game?

Informal requirements

According to Malcolm Evans, creator of the game and interviewed in that article about the making of 3D Monster Maze:

He rapidly developed a system that could generate 16x16 square mazes, each square either corridor or wall, and display this on the screen in a top-down view. With that done, there was still more to learn. Assembly language beckoned, so Evans added a routine to display what the maze look like for someone standing inside it.

I’m not interested in recreating 3D Monster Maze as such, although that would be an interesting experiment. So instead of thinking about blocks that are either corridor or wall, I want to instead think about tiles that represent spaces which might have walls on either side. This enables me to think, for now, about combinations of patterns and choices rather than a set of rules to determine something so binary. I may come back to the binary approach later.

Tiles

If we think of each tile being a square with four possible sides to “wall off”, there are sixteen different possible tile types, assuming that direction matters.

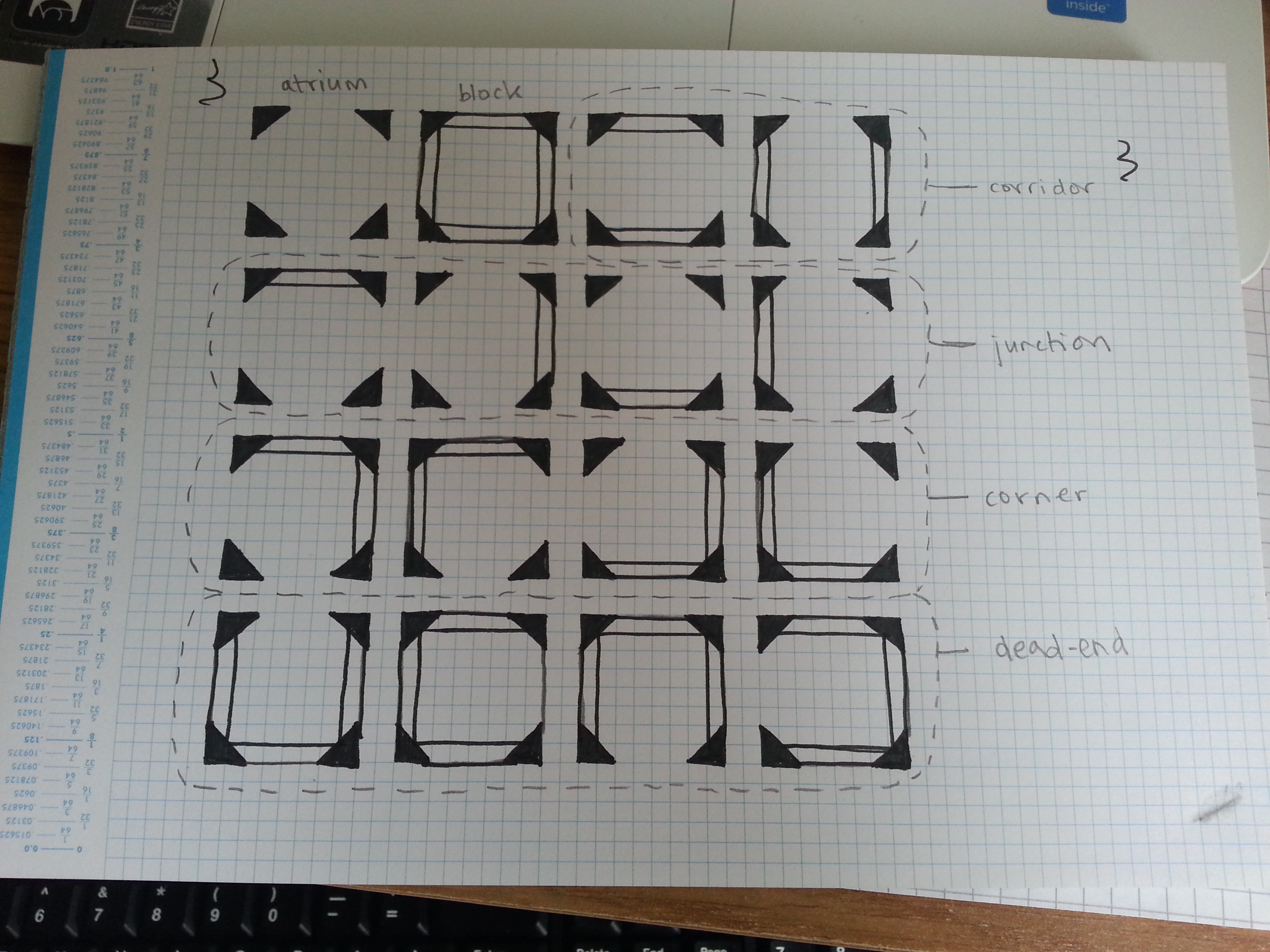
I drew out the groups of possible square tiles for this post to make them seem more tangible. Normally though, I'd just keep this visualisation in my head or scribble some sketches in a notebook.

If direction doesn’t matter, there are only six tile types: three that you can rotate three times for four different arrangements (junction, corner, and dead-end), one that you can rotate once for two different arrangements (corridor), and two to which rotation makes no difference at all (atrium and block).

We can use combinations of these tiles to create corridors or passageways.

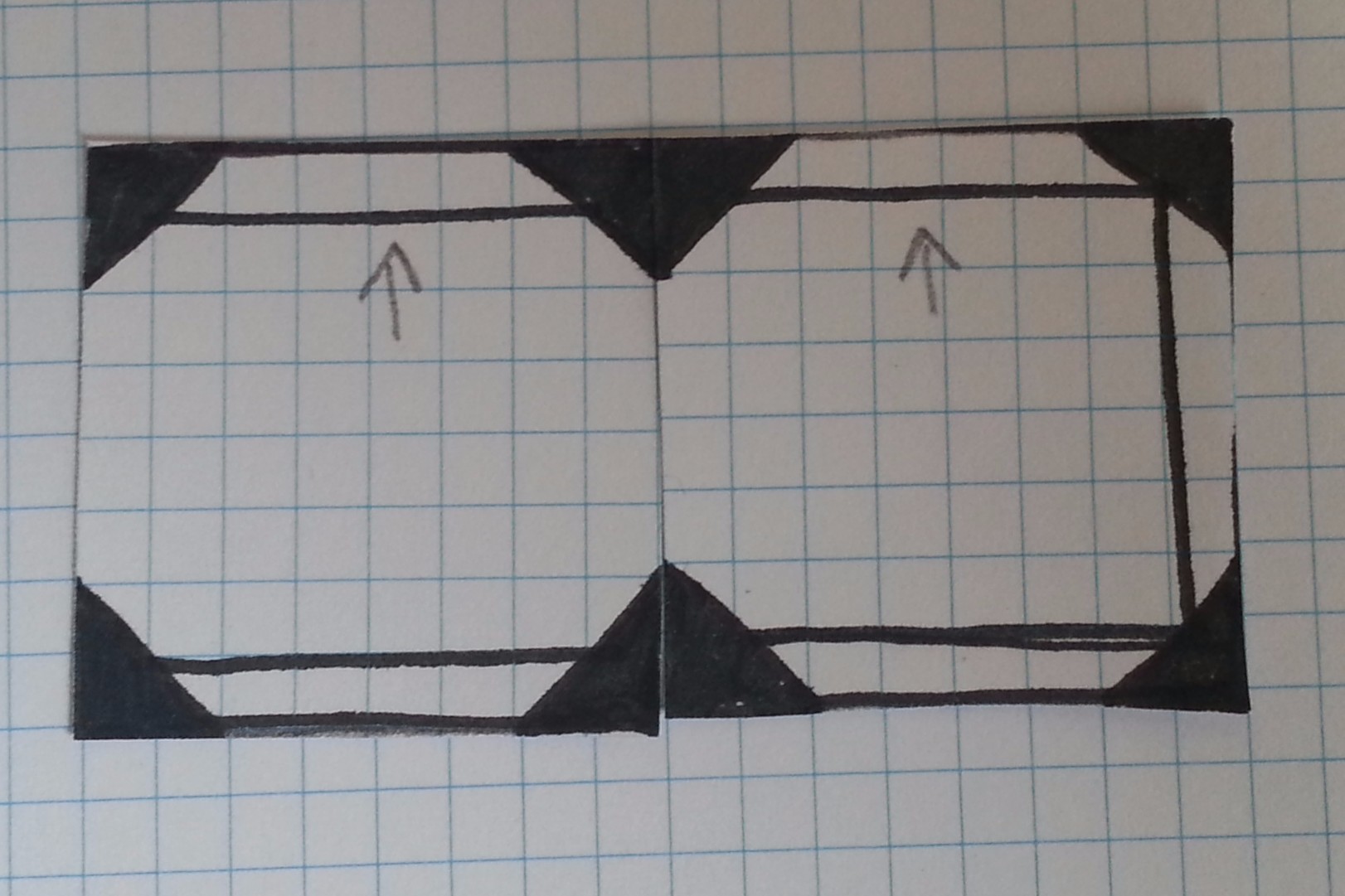
Two tiles can be arranged to create a very simple corridor. The arrows on the paper simply indicate which direction is "up" so tiles can be differentiated.

The more tiles we have the more complicated arrangements we can make.

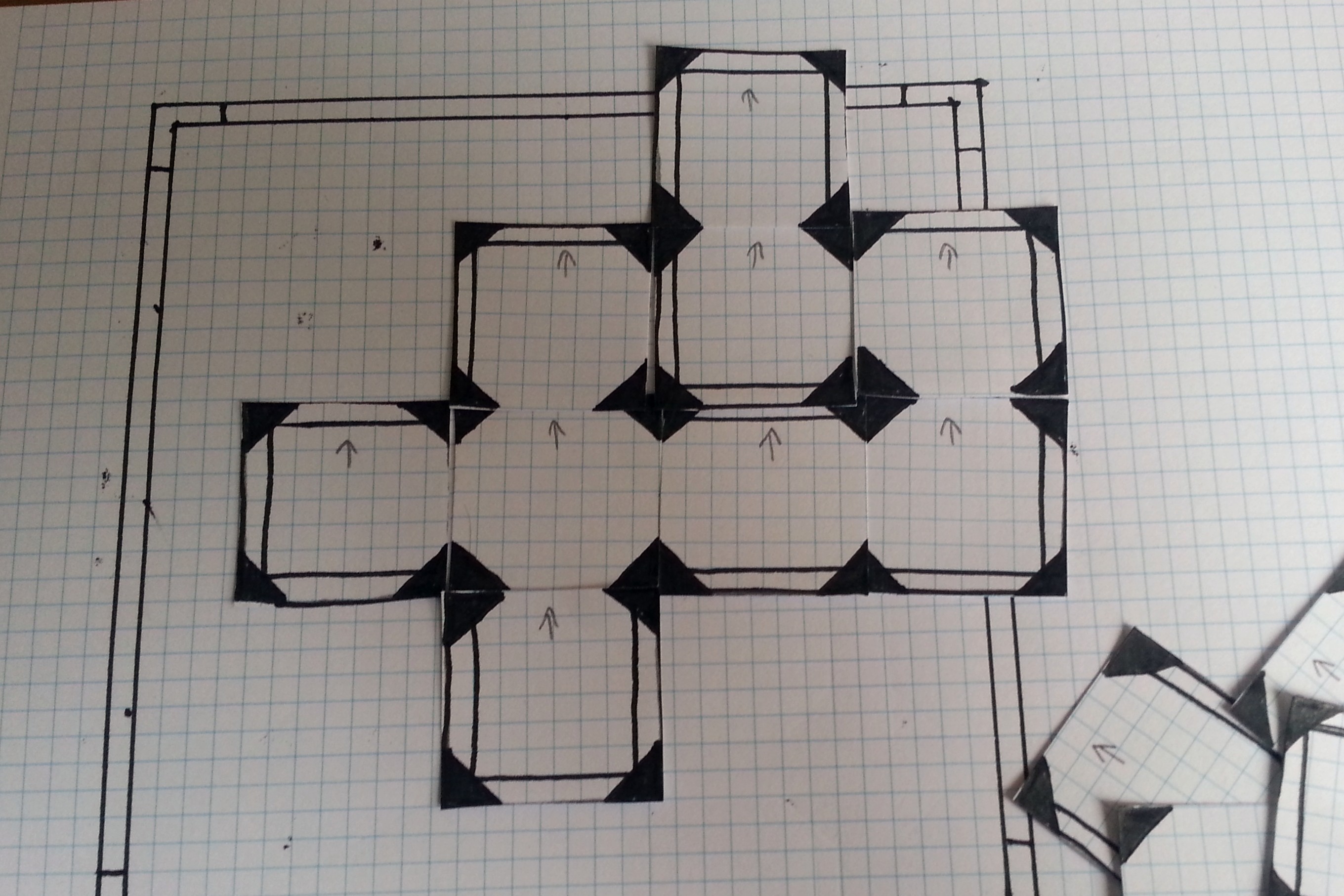
This is not a particularly impressive maze but it does give an idea of how combinations of tiles can come together.

However, if we’re completely randomising the arrangement of types of tiles we might need to be prepared for several unwanted openings around the edges. These could be blocked off by a general purpose wall that runs right around the edge of the maze.

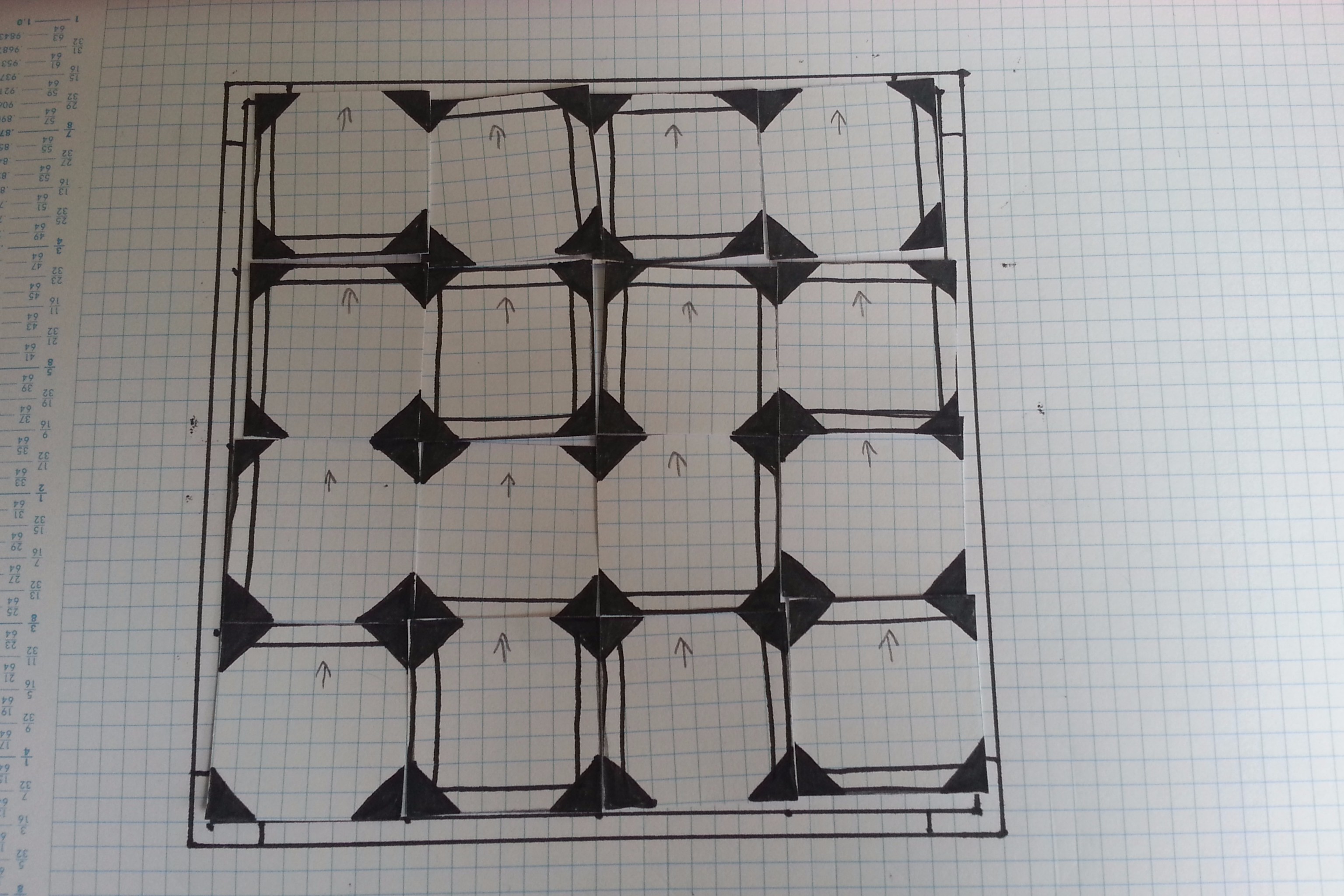
Here are the tiles randomly arranged within a wall. The pieces of paper proved quite fiddly at this point so this isn't as neat as I would have liked.

For simplicity’s sake we can decide right now that any maze generated should be square in shape. This makes the shape of the maze similar to the shape of the tile, and allows for a “maze” of one tile as an extreme case.

A way into the maze …

However, in all this, there is at least one other special tile type or feature we need to consider, if not two. Where does a “player” enter the maze and then, how does the player solve the maze?

The entrance or starting point for the maze seems essential (even if we decide it’s randomised).

An exit may not be essential. After all, it’s possible that the maze can be solved by returning to the entrance after a task has been achieved or by some other criteria, like having collected some items or covered some or all of the maze.

Once we’ve determined tile types, there’s then a question of whether or not there’s an optimal ratio of tile types and what arrangement of them works to make for an interesting game.

Quick summary of informal requirements

We can informally summarise the requirements for the tile-based maze like this:

  • The generated maze should be square.
  • There must be an entrance.
  • There might be an exit.
  • A wall on one tile can block off the opening of another.
  • Two adjacent walls behave the same as one. (This is an accepted redundancy.)

The problems of representation

I’ve mentioned different types of tiles and I even made some pen-on-paper sketches and mock-up arrangements. Now to think about how to represent the tiles in code.

I’m not referring to graphics in this case. The maze generated could be used for a first-person maze or a top-down view game. Malcolm Evans started with the latter when developing 3D Monster Maze and got to the former through exploration and experimentation.

Encoded tiles

We’re instead talking about how to represent the tiles and the overall maze in code. Once we’ve got an abstract way to do this, we have a way to work with the tiles and the maze – to rearrange them as needed and to try and work out what the optimal sets or arrangements are.

Each tile could be an encoded version of its walls. So a tile with no walls could be 0000 whereas a tile with a north wall could be 1000, an east wall 0100, a dead-end with a north opening 0111 and so on.

But a simpler representation would be to assign a letter to each tile. There are only sixteen tiles after all. That way each maze could be represented by a string of characters, which then makes it easy to test and manipulate.

We could simply label each of the sixteen tiles from a to p. Or we could come up with something more memorable like n, e, s, and w for tiles which have one wall in the north, east, south, and west respectively. Such a mnemonic system might prove easier to read.

Moving on for now

Ultimately though, for the purposes of experimenting with mazes programmatically, the actual letters themselves don’t matter so long as there’s a mapped set of conventions that can be interpreted.

All we need to know for now is that we have some options for representing the maze.

A “walk-through” function

If we’re going to randomly generate mazes based on sets of tiles, we need a way to test how effective the maze is and determine if there are particular sets or arrangements of tiles that generated better mazes than others. We can imagine and possibly build a “walk through” function.

Such a function should be able to go through any maze that meets our informal requirements, whether we create the maze manually or generate it automatically. But what do we need such a function to tell us?

Coverage

We need to know if every tile on the maze can be reached from the designated entry-point. That way, we know how much “redundancy” is part of any arrangement, or conversely how much coverage there is.

If we have an exit tile, we need to know if the exit can be reached by some route from the entry-point. In other words, we need to know whether it is actually possible to complete the maze.

Maze difficulty

Aside from trying to rule out impossible mazes, it would be good if the function could tell us how difficult the maze is. A maze that’s one long winding corridor isn’t much of a maze.

But how do we measure difficulty?

If each tile only ever has two open sides, the maze will probably be easy to solve – as a player, you then only have one direction to head in, namely the opposite direction to the way you came. A maze’s difficulty therefore should be about the choices it offers to you; you need to have to decide as a player and then remember your decisions.

On other hand, if we take this to the extreme and imagine that every tile has four sides open, then it really doesn’t matter which route you choose; you will be able to find the exit or navigate the maze quite quickly. The choices have to matter. So obscuring the visibility of the exit must also as must the distance one has to travel to reach it.

What to measure

So there are at least four things we can ask our function to tell us:

  1. Coverage
  2. Completion [if the maze has an exit]
  3. Minimum number of choices to see exit [once you have a visible path to the exit, there is no difficulty left]
  4. Distance to exit or distance to cover every tile

Finding the way from thinking and doing

This is naturally the point at which I would start doing. Having done some planning and thinking, I’m now at the point where I want to start coding and exploring.

When is the right time?

I should emphasise at this point that I don’t know if this is the right point to start work. It just feels right to me. Others might need or prefer to stay thinking about the problems and possible solutions longer until they have it all mapped out in their heads. For me, doing something at this point, actually getting some code written and testing the ideas is part of the fun. It also prevents inertia or paralysis or extreme procrastination.

It’s very easy to get stuck thinking about an idea, imagining the possibilities. At some point one needs to stop imagining and start making actual sketches to see if one’s idea is feasible.

Precrastination vs procrastination

As I was writing this post, I saw a TED talk on the suprising habits of original thinkers. I wasn’t looking for it but it showed up as a notification on my phone and I was curious enough to watch it. I’m not saying I’m a particularly original thinker but a lot in that talk resonated with me.

In thinking about the idea of a maze game I didn’t immediately start coding. I hesitated, held back and mulled it over. I drew sketches.

In the past, perhaps when I was naive about the number of problems one has to tackle when coding, I might have dived right in. But that’s when I was learning in a different way and playing with the code as I learned. It’s important to note that the thinking I’ve outlined above doesn’t constitute a plan as such. All I’ve done is thought about the sorts of problems I might encounter in trying to create such a game and about the kind of questions I really want to answer. This isn’t a good way to achieve high productivity! So I’m definitely not “precrastinating” in the way described in the video.

I don’t know if I’ve hit the “sweet spot” that Adam Grant talks about in his presentation. But I guess this is how Malcolm Evans worked when he was experimenting with the simple idea of a maze. As the article on the making of 3D Monster Maze makes clear, he did not originally have a game idea as such; he was exploring possibilities.

Others’ explorations

There’s a great video by Mattias Petter Johansson about the actual process of thinking, planning and coding. He dives into trying to solve an apparently simple problem and then finds all sorts of unexpected problems. In the end the video becomes an unexpected study on the surprises that programming can bring up and what the process actually feels like day-to-day.

There are a couple of interesting follow-up videos that show Matthias trying to take the project to completion. Mattias’ YouTube channel FunFunFunction is one of my favourite YouTube channels and is interesting not just for his explanations of coding concepts but also for his take on the philosophy and ethos of programming.

Next

So I’ve outlined the kind of thinking I do before I start coding

The next natural step would be to start to code up some of thoughts above. If I do, I’ll post it as a GitHub repository and write up the experience here.